数理最適化ソルバー活用事例｜組合せ最適化で社内交流会の班分けを自動化

こんにちは、調和技研研究開発部の貫洞です。私は現在、組合せ最適化に関する案件を担当しています。

今回は、数理最適化ソルバーを用いて身近な組合せ最適化問題を解決した事例を紹介します。組合せ最適化に関する説明は但野が書いた記事があるので、是非そちらをお読みください。

数理最適化ソルバーとは？

数理最適化ソルバーとは、複雑な問題を数学的に表現し、その最適解を算出するためのツールです。ソルバーは、設定された制約条件の下で目的関数を最小化または最大化することにより、最適な解を見つけます。

但野の記事で紹介されていたメタヒューリスティクス同様、数理最適化ソルバーは工業、運輸、財務などの様々な分野で用いられます。両者の特徴を比較すると以下の通りとなります。

解きたい問題の難易度や規模によって両者を使い分けるのが良さそうです。本稿では、数理最適化ソルバーを使用した問題解決の流れをご紹介します。

実際の課題を解いてみよう

では、私が調和技研の社内にあった課題を数理最適化ソルバーで解決した事例をご紹介します。

課題：社内メンバー交流会の班分け作成

弊社は基本的にフルリモートワークで、メンバーは全国に点在しています。メンバーは上長との月1回の1on1を行っていますが、その他のメンバーとは「お互いに会ったことがない」ということもよくあります。

そこで、研究開発部メンバー全員が対象で、メンバー間のコミュニケーション機会の創出を目的として、毎月1回、3～4人を1班としてメンバー交流会を行っています。

このメンバー交流会の班分けを決定することを考えます。実は、この交流会（以前は上長以外との1on1）の取り組みの開始当初は担当者が組分けを人手で行っていたのですが、これが結構大変です。班分けは完全ランダムで良いかというとそうではありません。まず、守らなければいけない制約として、

というものがあります。その上で、以下の目的もあります。

2023年11月時点で、研究開発部のメンバーは43人です。基本的に3人1班（3で割り切れない場合は4人班を作る）とすると、43人を4人×1班、3人×13班に分けることになりますが、その場合の全組合せ数は、なんと30952010052684060685304960000000通りあります。

この中から、上述の制約を満たし、最も目的に合致する「良い班分け」を人手で見つけ出すのは現実的ではありません。

実際、組分け担当者の方は1か月分の作成に数時間はかかっていたようです。しかも、本当に「良い組分け」が出来ているかも分かりません。そのような事情があり、ある日私は担当者から「組合せ最適化で何とかできないか」と相談を受けたというわけです。

課題を組合せ最適化問題として考えてみる

前述の通り、最適化ソルバーを利用するには問題を数学的に表現（＝定式化）する必要があります。定式化には、「決定変数（および補助変数）」、「制約条件」、「目的関数」が必要です。

加えて、今回使用するソルバー『SCIP[1]』では、他の多くのソルバーと同様、問題を「線形」で定式化する必要があります。もう少しわかりやすく言うと、「制約条件」や「目的関数」を「変数」で表現する際、変数同士の掛け算や、変数を引数とする非線形の関数が含まれる形で表現してはいけないということです。こちらに注意して、この課題を組合せ最適化問題として考えてみましょう。

では、「決定変数」、「制約条件」、「目的関数」を順番に見ていきます。

決定変数

この課題は、メンバーの集合を\( M = \{ 1, \ldots, m \}\)、班の集合を\( G = \{ 1, \ldots, g \}\) とすると、メンバー\( i \)が班\( j\)に割り振られる場合1、そうでない場合は0となるような\( m×g\) 個の0-1変数

\( x_{ij}, \quad i \in M, \, j \in G\)

の値の組合せ（＝班分け候補）\( \boldsymbol{x}\)の中から、変数間の制約を満たしかつ最も目的に合致する\( \boldsymbol{x}^{*}\)を決定する組合せ最適化問題とみることができます。

視覚的に表すと、以下の図1のようになります。1つのセルが1つの\( x_{ij}\)を表しており、図の例はメンバー1がグループ3、メンバー2がグループ1、…に割り当てられている組合せを表しています。

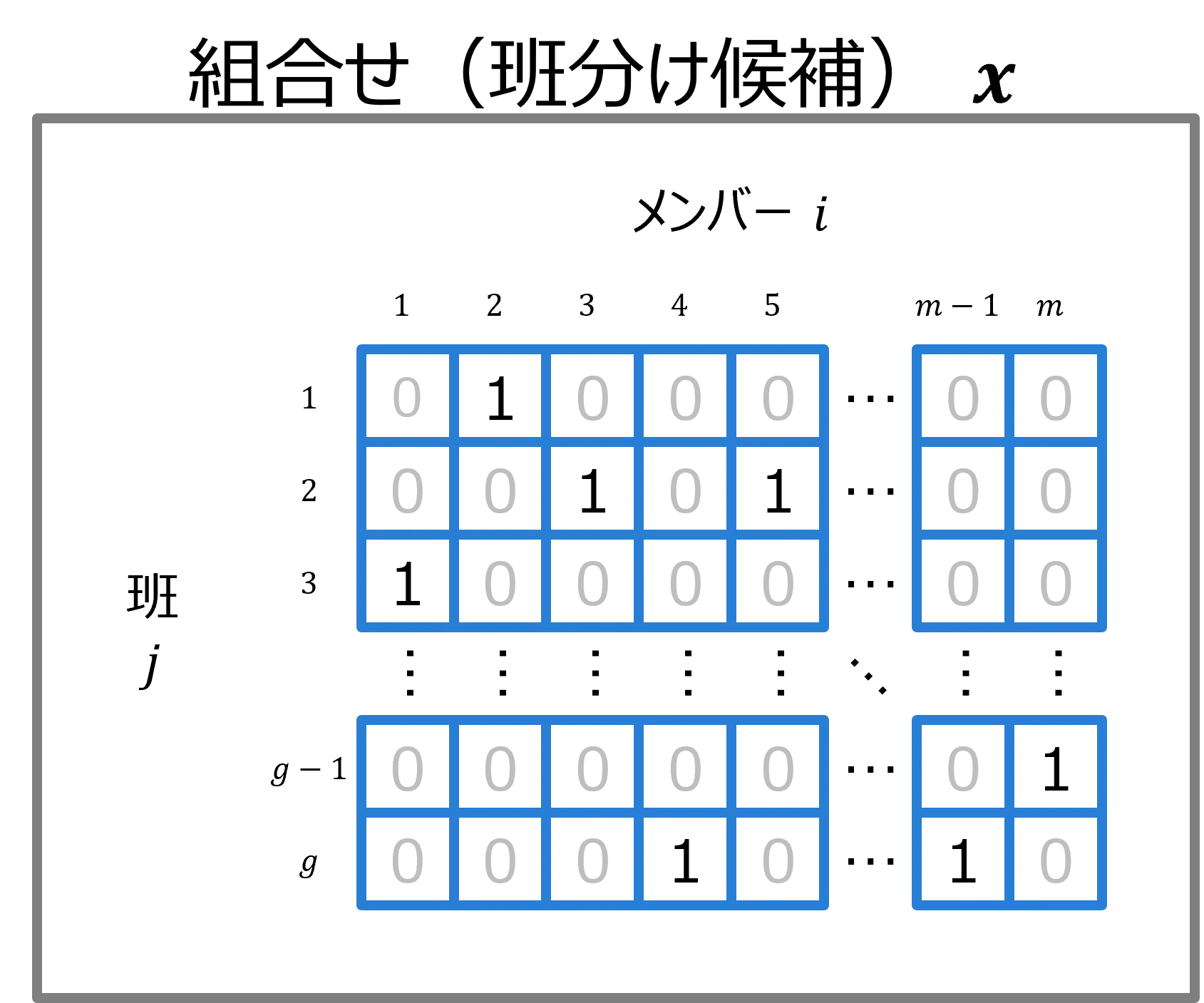図1

制約条件

この問題で考慮すべき制約条件も数式で表現していきましょう。ここでは、明示的に与えられている条件（例：上長と同じ班にならない）だけでなく、問題の前提となるような条件（例：各班の人数が決められている）も「制約条件」として扱います。

制約①：メンバーは、いずれかの班に振り分けられる

こちらの制約条件は、以下の2種類の制約式によって過不足なく表現できます。

• 制約①-(1)：全てのメンバー\(  i \)は、必ず1つの班\( j \)にのみ割り振られる

\( \sum_{j \in G} x_{ij} = 1, \quad i \in M\)

図1の全ての列（メンバー）について、1列の合計値が1であることに相当

•     制約①-(2)：全ての班\( j \) は、割り振られる人数\( N_j \)が決まっている

\( \sum_{i \in M} x_{ij} = N_j, \quad j \in G\)

図1の全ての行（班）について、1行の合計値が\( N_j \)であることに相当

制約②：全てのメンバー \( i \)は、そのメンバーから見た特定の1人のメンバー（＝上長）\( c_i \)とは同じ班にならない

こちらは、以下の制約式によって表現できます。

\( x_{ij} + x_{c_i j} \leq 1, \quad i, c_i \in M, \, j \in G\)

例えばメンバー1の上長がメンバー3だったとすると、全ての行（班）について、\( i=1\) と  \(  i=c_1=3\) のセルの値の合計が1以下であることに相当します。

ちなみに、ここまでに出てきている制約条件は全て変数について線形で表現できていますね。

目的関数

次に、「目的に合致する班分け」とはどのような班分けか、どうすれば班分け候補\( \boldsymbol{x}\)を定量評価できるか考えてみましょう。

前述の通り、メンバー交流会の目的は「今まで交流が少ない人同士が交流できる機会を作る」です。これは、言い換えると「今まで交流が多い人同士が同じ班にならないように班分けをしたい」となります。よって、今回は「最近の交流会で同じ班になったことがあるメンバーと再び同じ班になっているメンバーがいる班分け候補\( \boldsymbol{x}\)」であるほど値が大きくなるように目的関数\( f(\boldsymbol{x})\)を設計した上で、この最適化問題の目的を\( f(\boldsymbol{x})\)の最小化

\( \text{minimize: } f(x)\)

とすることとします。

まず準備として、補助変数 \( z_{uv}\)を用意します。この変数は、組分け候補\( \boldsymbol{x}\)においてメンバー\( u \)と\( v \)が同じ班になっていなければ0、なっていれば1を取る0-1変数であり、

\( z_{uv} = \sum_{j \in G} x_{uj} x_{vj}, \quad u, v \in M\)

という制約条件によって過不足なく表現できます。

　ここで、今回初めて変数同士の掛け算が出てきてしまいました。前述の通り、制約条件および目的関数を変数同士の掛け算で表現してはいけません。この問題は後ほど解決することにしましょう。

次に、過去の各月の班分け結果の記録から、どのメンバー同士がいつ同じ班になったかが分かるので、2人のメンバー\( u \)と\( v \)が最近同じ班になっているほど大きな値となるように定数\( p_{uv}\)を定義します（値の計算方法は今回の主題ではないので割愛します）。

そして、ある今月の組分け候補\( \boldsymbol{x}\)に対する目的関数\( f(\boldsymbol{x})\)を、

\(f(\boldsymbol{x}) = \max\limits_{u \in M} \sum_{v \in M} p_{uv} z_{uv}\)

とします。\( f(\boldsymbol{x})\)を

\( \sum_{u \in M} \sum_{v \in M} p_{uv} z_{uv}\)

としなかった理由は、特定のメンバーの\( p_{uv} z_{uv}\)が大きくなってしまうことを防ぐためです。最大値を最小化することで、全メンバーの\( p_{uv} z_{uv}\)をバランスよく小さくすることができます。

しかし、上述の通り目的関数にmax関数を使用するメリットはあるものの、max関数は「非線形」な関数です。先ほどの変数同士の掛け算といい、この表現のままではソルバーに渡すことができません。この問題も後ほど解決しましょう。

式からわかる通り、\( f(\boldsymbol{x})\)は組分け候補\( \boldsymbol{x}\)の中に1人でも「最近同じ班になったメンバーと再び同じ班になっているメンバー」がいると大きな値となってしまいます。言い換えると、\( f(\boldsymbol{x})\)が小さい組分け候補\( \boldsymbol{x}\)ほど、「最近同じ班になったメンバーと再び同じ班になっているメンバーがいない」＝「良い組分け」である、ということができます。

上記のように、どのような解が「得たい解」であるかを検討し、それを定量的に表現するところは人間が行う必要があります。目的関数は、文字通り目的に合わせて適切に設計しましょう。

制約条件・目的関数の線形化

上記で定式化が完了したように見えますが、忘れてはいけないことがあります。まず、補助変数\( z_{uv}\)に課せられている制約が変数同士の掛け算で表現されています。また、目的関数\( f(\boldsymbol{x})\)にはmax関数が使われています。これらはどちらも線形な表現ではありません。前述の通り、最適化ソルバーSCIPを使用するには全ての制約条件・目的関数が変数について線形で表現されている必要があります。よって、これら非線形な式を等価な線形の式に変形していきましょう。

◾️目的関数\( f(\boldsymbol{x}) = \max\limits_{u \in M} \sum_{v \in M} p_{uv} z_{uv}\)の線形化

今回の問題はmax関数が使われている目的関数の最小化問題なので、最大値最小化問題となります。このケースの場合、新しく補助変数\( y\)を用意し、以下のような制約を設定した上で\( y\)を目的関数と再設定し、目的を\( y\)の最小化

\(  \text{minimize: } y\)

とすることで、元の最適化問題と等価な線形表現に変形することができます。ただし、\( y\) は以下のような線形表現の制約が設定されます。

\( \sum_{v \in M} p_{uv} z_{uv} \leq y, \quad u \in M\)

◾️\( z_{uv} = \sum_{j \in G} x_{uj} x_{vj}, \quad u, v \in M\)の線形化

こちらは\( x_{uj} x_{vj}\)の部分（論理式で言うAND）が変数同士の掛け算、すなわち非線形となっているので、線形化する必要があります。変数\( x_{ij}\)が0-1変数であるので、新たに

\( w_{uvj}, \quad u, v \in M, \, j \in G\)

という0-1変数を用意し、以下のような制約を設定することで\( x_{uj} x_{vj}\)と等価な値を線形の制約のみで表現することができます。 

\( 2w_{uvj} \leq x_{uj} + x_{vj}, \quad u, v \in M, \, j \in G\)

\( x_{uj} + x_{vj} \leq w_{uvj} + 1, \quad u, v \in M, \, j \in G\)

これにより\( z_{uv} = \sum_{j \in G} w_{uvj}\)と変形できるので、\( y \)に対する制約条件も\( z_{uv}\)を使わず

\( \sum_{v \in M} \left( p_{uv} \sum_{j \in G} w_{uvj} \right) \leq y, \quad u \in M\)

と表現することができます。

以上で、今回の問題の定式化は完了です。改めて全ての変数・制約条件・目的関数について整理します。全ての制約条件・目的関数が変数について線形で表現できていますね。

変数

• \( x_{ij}, \quad i \in M, \, j \in G\)
• \( y\)
• \( w_{uvj}, \quad u, v \in M, \, j \in G\)

制約条件

• \( \sum_{j \in G} x_{ij} = 1, \quad i \in M\)
• \( \sum_{i \in M} x_{ij} = N_j, \quad j \in G\)
• \( x_{ij} + x_{c_i j} \leq 1, \quad i, c_i \in M, \, j \in G\)
• \( \sum_{v \in M} \left( p_{uv} \sum_{j \in G} w_{uvj} \right) \leq y, \quad u \in M\)
• \( 2w_{uvj} \leq x_{uj} + x_{vj}, \quad u, v \in M, \, j \in G\)
• \( x_{uj} + x_{vj} \leq w_{uvj} + 1, \quad u, v \in M, \, j \in G\)

目的関数

• \( \text{minimize: } y\)

あとは、この定式化結果を実装してソルバーでの最適化を実行するだけです。

最適化結果

最適化結果の例を示します。11月のメンバー交流会の割り当て結果は以下の図2のようになりました（こちらは実際に使用した班分け結果ですが、プライバシーに配慮してメンバー名は全て仮名としています）。

図2

縦軸・横軸はメンバー\( u\)と\( v\)を表しており、図中の縦軸が\( u\)、横軸が\( v\)となっているマスに記載されている数値は\( p_{uv}\)を表しています。\( p_{uv}\)の値が0となっているような\( u\),\( v\)は先月までに一度も交流会で同じ班になったことがないことを意味し、逆に値が大きければ大きいほど、最近（1on1を行っていたり）交流会で同じ班になったことがあることを意味します。

具体的には、（計算の詳細は割愛しますが）\( u\),\( v\)が1か月前に同じ班になっている場合は\( p_{uv}＝\)1.0、12か月前に同じ班になっている場合は約0.14となっています。

\( p_{uv}\)のマスに色付きの印（2～3個）が付いている列に対応するメンバーが、今月の交流会で同じ班に割り振られたメンバーを表しています。例えば、メンバー1はメンバー18、メンバー23と3人で交流会を行うということです。図を見ると、どのメンバー\( v\)の 1行の色付きのマスの合計\(  \sum_{v \in M} \left( p_{uv} \sum_{j \in G} w_{uvj} \right)\)も0.14以下となっていることがわかります。これは、メンバー43人全員が、少なくとも最近1年以上同じ班になっていない（つまり交流の少ない）メンバーのみと同じ班になっていることを意味します。ちなみにこの結果を得るまでの計算時間は、一般的なノートPCを利用して8分弱でした（「最適解」を見つけたわけではなく、実用的な解の目的関数が0.14程度だと分かっているので、それ以下の値が得られた時点で計算を完了としています）。

つまり、組合せ最適化ソルバーを使用することによって、目的に合致する「良い班分け」を短時間で作成できたということが言えます。

あなたの抱えている問題も解決できるかも？

本稿では身近な課題を数理最適化ソルバーの利用によって解決した例をご紹介しました。

今回の課題は変数・制約がともに非常に少ない比較的簡単な問題でしたが、大規模・複雑な課題も解決までのプロセスは変わりません。

調和技研では、最適化技術を用いたAIの開発実績が多くあり、シフト作成、ルート選定、献立の自動作成など、企業様ごとの様々な課題解決をご支援しています。あなたが抱える課題も最適化で解決できるかもしれません。ぜひお気軽にご相談ください。

＞＞調和技研のオーダーメイドAI開発・導入支援サービス

【参考文献】

[1] SCIP